Mảng một chiều trong Java

Được viết bởi: phuongle (SMod)

Bình luận: 0
0 Lượt chia sẻ
Lượt xem

Độ khó

Dễ

Số bước

Thời gian

Chia sẻ

1. Giới thiệu chung về mảng

Trong Java cũng như các ngôn ngữ lập trình khác, mảng là kiểu dữ liệu có cấu trúc gồm một tập hợp cố định các phần tử có cùng kiểu dữ liệu, các phần tử của mảng có cùng tên và được phân biệt nhau bởi chỉ số. Mỗi phần tử của mảng được sử dụng như là một biến đơn, kiểu dữ liệu của mảng chính là kiểu dữ liệu của phần tử. Như vậy, đối với mảng thì chúng ta cần quan tâm đến các thành phần sau:

Các thông tin liên quan đến mảng: tên mảng, số phần tử của mảng, kiểu dữ liệu của mảng.
Số chiều của mảng: Nếu mảng chỉ có một chỉ số để lưu trữ các giá trị vào trong các biến thành phần của mảng thì được gọi là mảng một chiều. Nếu mảng có 2 chỉ số để lưu trữ các giá trị (chẳng hạn giá trị của một bảng có m dòng, n cột) được gọi là mảng 2 chiều. Tương tự, ta có mảng 3 chiều, 4 chiều, …, n chiều.

Trong lập trình, mảng thường xuyên được sử dụng không chỉ bởi tính đơn giản, dễ sử dụng của nó mà còn ở khả năng đáp ứng nhu cầu lưu trữ dữ liệu trong các bài toán thực tế. Chúng ta có thể sử dụng mảng khi cần lưu trữ nhiều giá trị, chẳng hạn như lưu trữ các số nguyên từ 1 đến 5; dãy 32 chuỗi ký tự, trong đó mỗi chuỗi lưu trữ tên của một sinh viên trong một lớp học…

Trong Java, mảng được hỗ trợ dưới dạng mảng một chiều cho đến mảng nhiều chiều. Nhưng thông thường, khi lập trình chúng ta thường chỉ sử dụng mảng có tối đa là ba chiều và mảng một chiều là mảng được sử dụng nhiều nhất. Trong chương này, tôi sẽ hướng dẫn các bạn tìm hiểu về mảng một chiều và mảng hai chiều, khi đã nắm chắc được 2 khái niệm này thì các bạn có thể làm việc với các loại mảng có số chiều nhiều hơn. Sau đây, chúng ta sẽ đi vào phần nội dung chính của bài này, đó là khái niệm, cú pháp khai báo, cách sử dụng và các phương thức của mảng một chiều và ví dụ vận dụng.

2. Mảng một chiều trong Java

Mảng một chiều là một tập hợp của nhiều phần tử có kiểu dữ liệu giống nhau.

Cú pháp khai báo mảng

Để khai báo mảng, chúng ta cần phải xác định trước 3 thông tin cần thiết sau:

Kiểu dữ liệu của mảng.
Tên của mảng.
Số lượng các phần tử (hay kích thước) của mảng.

Câu lệnh khai báo mảng sẽ có 2 dạng như sau:

Dạng 1:

[Kiểu_dữ_liệu] tên_mảng[];

Dạng 2:

[Kiểu_dữ_liệu][] tên_mảng;

trong đó, <tt>[Kiểu_dữ_liệu]</tt> mô tả kiểu của mỗi phần tử thuộc mảng (như int, char, double, String,…), tên_mảng là tên của mảng và quy tắc đặt tên phải tuân theo quy tắc đặt tên biến trong Java.

Ví dụ: int[] a;: khai báo mảng tên a và có kiểu dữ liệu là int.

Cấp phát bộ nhớ cho mảng

Tương tự như chuỗi, bản chất của mảng là 1 đối tượng (chi tiết về đối tượng chúng ta sẽ được học trong chương Lập trình hướng đối tượng), vì vậy mảng cần phải được cấp phát bộ nhớ trước khi sử dụng. Để cấp phát bộ nhớ cho mảng thì chúng ta có 2 cách như sau:

Cách 1: [Kiểu_dữ_liệu] tên_mảng[] = new [Kiểu_dữ_liệu] [Số_phần_tử_của_mảng];

Cách 2: [Kiểu_dữ_liệu][] tên_mảng = new [Kiểu_dữ_liệu] [Số_phần_tử_của_mảng];

trong đó, [Số_phần_tử_của_mảng] chỉ ra số lượng phần tử tối đa mà mảng có thể lưu trữ, giá trị này phải là một số nguyên dương.

Ngoài ra, Java còn cho phép chúng ta vừa có thể khai báo mảng và vừa khởi tạo giá trị cho mảng, ví dụ:

int[] a = new int[] {2, 10, 4, 8, 5};: khai báo mảng một chiều có tên là a, kiểu dữ liệu là int và mảng này chứa 5 phần tử có giá trị lần lượt là 2, 10, 4, 8, 5.

Truy xuất các phần tử của mảng

Đối với mảng thì chúng ta có thể truy xuất các phần tử của mảng thông qua các chỉ số của phần tử đó. Cú pháp như sau:

Tên_mảng[Chỉ_số_phần_tử];

trong đó, [Chỉ_số_phần_tử] là số thứ tự của các phần tử trong mảng và bắt đầu từ 0. Như vậy, mảng có n phần tử thì các phần tử của nó có chỉ số lần lượt là 0, 1, 2,…, n – 1.

Ví dụ: Chúng ta có đoạn chương trình sau:

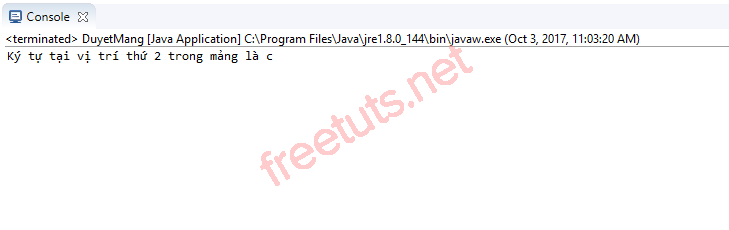
public static void main(String[] args) {
    // Khai báo và khởi tạo giá trị ban đầu cho mảng
    char[] kyTu = new char[] {'a', 'b', 'c', 'd', 'e'};
        
    // hiển thị ký tự tại vị trí thứ 2 trong mảng
    System.out.println("Ký tự tại vị trí thứ 2 trong mảng là " + kyTu[2]);
}

Kết quả sau khi biên dịch chương trình:

3. Nhập xuất các phần tử cho mảng

Chương trình dưới đây sẽ minh họa cách nhập các phần tử cho mảng một chiều từ bàn phím và sau đó hiển thị các phần tử đó ra màn hình.

Ví dụ

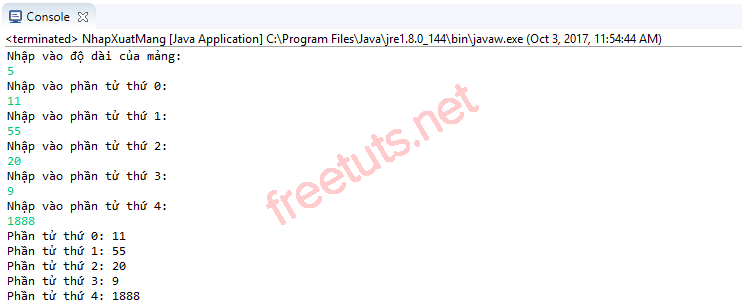
public static void main(String[] args) {
    int size;   // kích thước của mảng
    Scanner scanner = new Scanner(System.in);
        
    System.out.println("Nhập vào độ dài của mảng: ");
    size= scanner.nextInt();
        
    // khai báo và cấp phát bộ nhớ cho mảng
    // mảng này có tên là array và kích thước = size
    int[] array = new int[size];
        
    // array.length: trả về kích thước của mảng
    // vòng lặp này sẽ duyệt i từ 0 đến chiều dài của mảng - 1
    for (int i = 0; i < size; i++) {
        System.out.println("Nhập vào phần tử thứ " + i + ": ");
        array[i] = scanner.nextInt();   // nhập giá trị cho phần tử
    }
        
    // hiển thị giá trị các phần tử trong mảng
    for (int i = 0; i < size; i++) {
        System.out.println("Phần tử thứ " + i + ": " + array[i]);
    }
}

Kết quả sau khi biên dịch chương trình:

4. Một số thao tác đối với mảng một chiều

Gán giá trị cho phần tử của mảng

Cho 2 mảng array1 và array2 là các mảng có cùng kiểu dữ liệu. Giả sử các phần tử trong mảng array1 đã có giá trị, khi đó chúng ta có thể gán giá trị của một phần tử trong array1 cho một phần tử trong mảng array2 như sau:

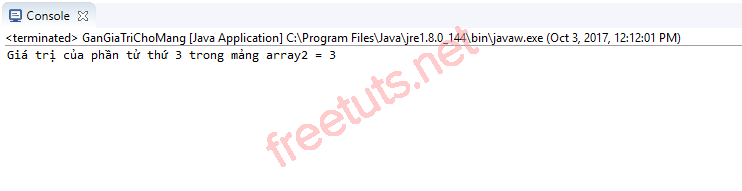
public static void main(String[] args) {
    // khai báo mảng array1 và array2
    int[] array1 = {2, 10, 3, 9, 8};
    int array2[] = new int[5];
        
    // gán giá trị của phần tử thứ 2 trong mảng array1
    // cho phần tử thứ 3 trong mảng array2
    array2[3] = array1[2];
        
    System.out.println("Giá trị của phần tử thứ 3 trong mảng array2 = " +
        array2[3]);
}

Kết quả sau khi biên dịch chương trình:

Sắp xếp các phần tử của mảng

Viết chương trình thực hiện các công việc sau:

Nhập liệu cho mảng A có n phần tử nguyên từ bàn phím.
Sắp xếp mảng số đã nhập tăng dần theo giá trị của các phần tử có trong mảng.
In ra màn hình mảng số ban đầu và mảng đã sắp xếp theo thứ tự tăng dần.

Yêu cầu kỹ thuật: Chương trình phải kiểm tra n nhập vào (n >= 2 và n <= max – 1, với max là số phần tử tối đa của mảng).

Bài giải

public static void main(String[] args) {
    int n, temp, max = 100;
    Scanner scanner = new Scanner(System.in);
        
    // khai báo và cấp phát bộ nhớ cho mảng A
    int A[] = new int[max];
        
    // nhập số phần tử của mảng
    // kiểm tra nếu n <= 2 hoặc n > max - 1
    // thì phải nhập lại
    do {
        System.out.println("Nhập số phần tử của mảng: ");
        n = scanner.nextInt();
    } while (n <= 2 || n > max-1);
        
    System.out.println("Nhập giá trị cho các phần tử của mảng: ");
    for (int i = 0; i < n; i++) {
        System.out.print("A[" + i + "] = ");
        A[i] = scanner.nextInt();
    }
        
    // in ra màn hình mảng số ban đầu
    System.out.println("Mảng ban đầu: ");
    for (int i = 0; i < n; i++) {
        // in các phần tử trên cùng 1 dòng
        System.out.print(A[i] + "\t");
    }
        
    // sắp xếp các phần tử trong mảng
    // vòng lặp for sẽ duyệt i và j
    // i chạy từ 0 đến n - 2, j chay từ i + 1 đến n - 1
    // nếu phần tử tại chỉ số j nhỏ hơn phần tử tại i
    // thì sẽ hoán đổi vị trí 2 phần tử này cho nhau
    for (int i = 0; i < n - 1; i++) {
        for (int j = i+1; j <= n - 1; j++) {
            if (A[j] < A[i]) {
                temp = A[i];
                A[i] = A[j];
                A[j] = temp;
            }
        }
    }
        
    // in ra màn hình mảng số sau khi sắp xếp
    System.out.println("\nMảng sau khi sắp xếp: ");
    for (int i = 0; i < n; i++) {
        System.out.print(A[i] + "\t");
    }
}

Kết quả sau khi biên dịch chương trình:

Phương pháp sắp xếp được sử dụng trong ví dụ trên có tên gọi là “Sắp xếp thông qua phép đổi chỗ trực tiếp” (Exchange sort). Đây là cách sắp xếp kém hiệu quả nhưng lại rất đơn giản và dễ hiểu. là phương pháp sắp xếp cơ bản nhất trong tất cả các phương pháp.

Tìm kiếm phần tử của mảng theo một điều kiện cho trước

Viết chương trình thực hiện các công việc sau:

Nhập liệu cho mảng có n phần tử nguyên (n > 0) từ bàn phím.
Nhập số nguyên k từ bàn phím.
Tìm kiếm phần tử đầu tiên trong mảng có giá trị bằng k và thông báo lên màn hình vị trí của phần tử đó. Nếu không có phần tử nào của mảng có giá trị bằng k thì thông báo “Trong mảng không có phần tử nào chứa giá trị cần tìm.“

Yêu cầu kỹ thuật: Chương trình phải kiểm tra n nhập vào: nếu n <= 0 hoặc n > số phần tử tối đa của mảng thì yêu cầu nhập lại số phần tử cho đến khi thỏa mãn điều kiện.

Bài giải

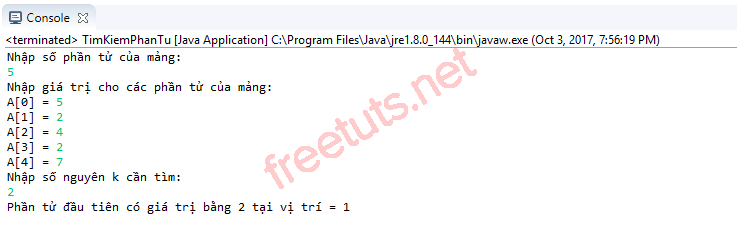
public static void main(String[] args) {
    int n, max = 100, i;
    int[] A = new int[max];
    Scanner scanner = new Scanner(System.in);
        
    do {
        System.out.println("Nhập số phần tử của mảng: ");
        n = scanner.nextInt();
    } while (n <= 0 || n > max - 1);
        
    System.out.println("Nhập giá trị cho các phần tử của mảng: ");
    for (i = 0; i < n; i++) {
        System.out.print("A[" + i + "] = ");
        A[i] = scanner.nextInt();
    }
        
    System.out.println("Nhập số nguyên k cần tìm: ");
    int k = scanner.nextInt();
        
    i = 0;
    // tiến hành tìm kiếm phần tử
    // nếu không tìm thấy giá trị tại i bằng với số nguyên k
    // thì tăng i lên 1
    while ((i < n) && (A[i] != k)) {
        i++;
    }
        
    // Nếu i lớn hơn số phần tử của mảng - 1
    // thì thông báo không tìm thấy phần tử
    // ngược lại hiển thị ra i
    if (i > n-1) {
        System.out.println("Trong mảng không có phần tử nào chứa giá trị cần tìm.");
    } else {
        System.out.println("Phần tử đầu tiên có giá trị bằng " + k + " tại vị trí = " + i);
    }
}

Kết quả sau khi biên dịch chương trình:

Phương pháp tìm kiếm được sử dụng trong ví dụ này được gọi là tìm kiếm tuần tự. Với phương pháp thì trong trường hợp xấu nhất có thể có đến n phép so sánh, tuy nhiên đây cũng là 1 cách tìm kiếm cơ bản nhất mà bất cứ lập trình viên nào cũng nên biết và sử dụng được nó.

5. Lời kết

Đây là bài tìm hiểu về kiểu mảng đầu tiên trong Java đó là mảng một chiều. Như đã nói, nội dung của bài này khá dài và khá phức tạp nên tôi sẽ không trình bày quá nhiều vì như vậy sẽ dễ làm cho các bạn khó nắm bắt được nội dung của bài. Để giúp các bạn có thể luyện tập tốt hơn về mảng một chiều trong Java, tôi sẽ bổ sung một số bài tập và cố gắng giải thích kỹ để các bạn có thể nắm chắc hơn nội dung về mảng. Các bạn theo dõi nhé!

Theo: freetuts.net